Problème de flot maximum

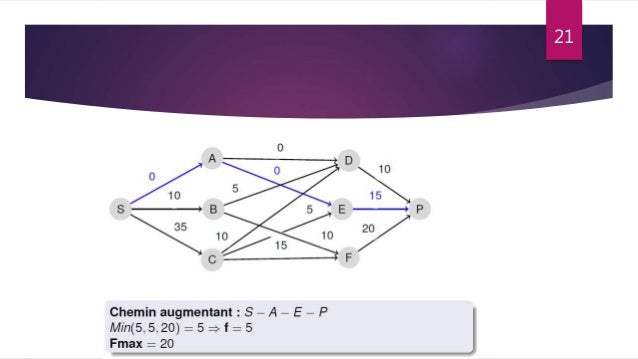
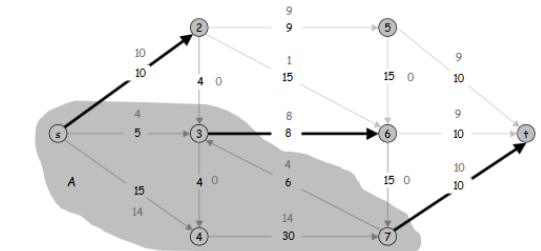
Le problème de flot maximum consiste à trouver, dans un réseau de flot, un flot réalisable depuis une source unique et vers un puits unique qui soit maximum. Quelquefois^[Quand ?], on ne s'intéresse qu'à la valeur de ce flot. Le s-t flot maximum (depuis la source s vers le puits t) est égal à la s-t coupe minimum du graphe, comme l'indique le théorème flot-max/coupe-min.

Applications

Ce type de problème est proche de ce qui est rencontré dans le remplissage optimisé de boîtes. On peut également utiliser des approches de flot maximum pour résoudre des problèmes de gestion d'écoulements dans des réseaux (égouts, conduites d'eau, trafic routier...).
Durant la Guerre froide, le problème de flot maximum est utilisé par l'US Air Force afin d'impacter au maximum le réseau ferré de l'Union Soviétique.

Algorithmes

Étant donné un graphe orienté $G=(V,E)$ , où chaque arc $u,v$ a une capacité $c(u,v)$ , on cherche un flot maximum $f$ depuis la source $s$ vers le puits $t$ , sous contrainte de capacité. Différents algorithmes ont été développés pour résoudre ce problème de complexités différentes. On utilise, dans la description des complexités, la notation simplifiée qui remplace le cardinal d'un ensemble par l'ensemble lui-même : on écrit $O(VE^{2})$ au lieu de $O(|V||E|^{2})$ .

Une liste plus complète figure dans le livre de Cormen, Leiserson, Rivest et Stein. Le problème du flot maximal est complet pour la classe P.

Extensions

Le problème du flot maximum peut être vu comme un cas particulier de plusieurs autres problèmes de flots dans les réseaux, comme le flot multi-commodités.

Références bibliographiques

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Maximum flow problem » (voir la liste des auteurs).